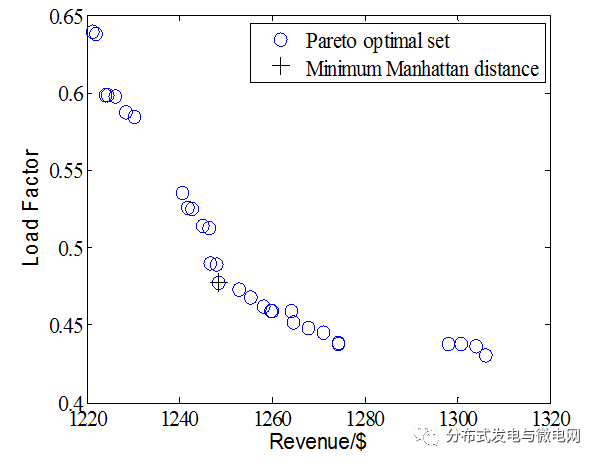
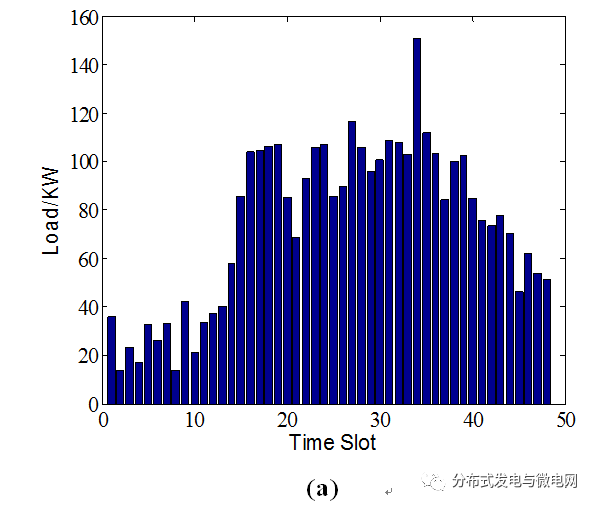
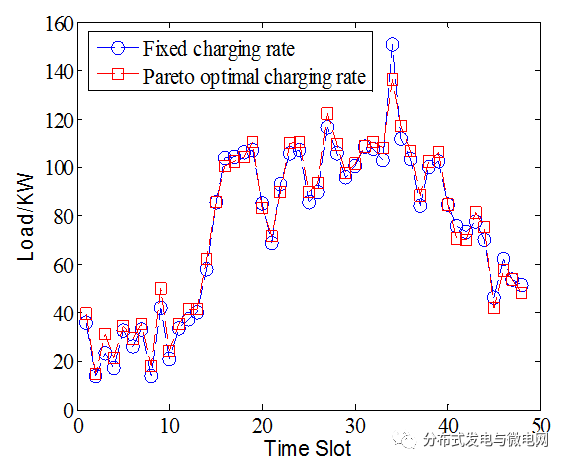
Researchers from the School of Electrical Engineering and Automation, Fuzhou University, and the Department of Electrical Engineering, Yuanzhi University, Taiwan, Guan Yuliang, Wang Jinhua, Qiu Weiyu, in the 12th issue of Electrical Technology magazine in 2017, this paper considers electric vehicles and electric vehicles in the smart grid. Charge scheduling problem for taxis. The charging station can control the charging rate to maximize its revenue; for the underlying power system, it is desirable to maximize its own load factor to ensure system stability. The charging station maximizes its revenue and power system maximizes its load factor to form a multi-objective optimization problem. This paper proposes a multi-objective optimization method to solve this multi-objective optimization problem, and then generate a Pareto optimal electric vehicle charging strategy. At the end of the paper, numerical analysis was carried out to verify the effectiveness of the proposed method. In recent years, with the deepening of the global energy crisis, the depletion of petroleum resources, air pollution, and rising global temperatures, governments and automobile companies are generally aware that saving energy and reducing harmful emissions are future automotive technologies. The inevitable direction of development [1]. The development of electric vehicles is a way to solve the above problems [2], however, the large number of electric vehicles connected to the grid will increase the overall burden of the grid. It is estimated that by 2050, the number of electric vehicles in China will reach 200 million, and the total charge will reach 330 million kilowatts [3]. The sharp increase in electric vehicles will have an important impact on China's power supply. For different electricity price collection modes, electric vehicles will have different charging requirements and will receive power supply from the grid at different times. The grid and electric vehicle trading models will become increasingly complex, requiring a more advanced power market to support this change [4]. With the large-scale growth of electric vehicles, it is particularly important to study the charging schedule and charging rate of charging stations. As the operator of the grid system, the charging station will first contact the electric vehicle users. It can adjust the grid load of each charging station by optimizing the charging rate of each charging station of the charging station to maintain the grid stability [5]. This paper is divided into several parts to discuss related topics: firstly discuss the mathematical model of the charging station and its service objects, then introduce the electricity price strategy under the smart grid mode, and finally discuss the corresponding multi-objective optimization problem and propose a solution. For the convenience of display, this article takes 30 minutes as a time slot and divides the day into 48 time slots. 1 Discussion of charging station and its service objects (omitted) 1.1 Charging station scale The importance of the charging station in the future society is similar to that of the current gas station. In order to adjust the amount of electricity load at each charging station, the charging station can regulate the charging rate of the household electric vehicle. The charging rate ranges from 5kw/h to 15kw/ h. The simulated charging station used in this paper has 20 charging piles per charging station, and can charge up to 20 electric vehicles at the same time for charging. Electric vehicles that are charged at a charging station include Plug-in Electric Taxi (PET) and household electric vehicles. 1.2 plug-in electric taxi 1.3 Household electric vehicles 2 Smart grid price strategy The grid company will guide the consumers to transfer peak electricity consumption by changing the price of electricity. The common electricity price models are: Real-timepricing, Day-ahead pricing, and time-of-use tariff (Time). -of-usepricing), Peak-time rebate pricing, etc. [10-13]. This article uses the price announced on May 25, 2017 by Maryland Interconnected Power Company (PJM) in Pennsylvania, USA (the electricity price announced on the previous day), and the unit price of the electricity price system during peak hours and off-peak hours is not the same [14] . This paper divides the hourly electricity price equivalent into two time periods, and discusses 48 time periods in a day, and uses the multi-objective optimization method introduced later to do related numerical simulation and analysis. 3 system flow and multi-objective optimization problem (omitted) 3.1 System Process As an important part of the smart grid, the charging station collects information such as the number of electric vehicles charged to the charging station, the remaining capacity of the battery and its charging requirements at various times. Then, the information is uploaded to the cloud, and unified optimization processing is performed by the computer dispatching center, and the optimal value of the charging rate of the household electric vehicle should be given to each charging pile at different time periods. Finally, the computer dispatch center feeds back the results to the charging station, and the charging station arranges the home electric vehicle for charging according to the optimization information. Figure 3 is a flow chart of the operation of the charging station in the smart grid mode. Figure 3 Charging station operation flow chart in the smart grid 3.2 Multi-objective optimization problem The multi-objective problem in this paper involves maximizing the charging service revenue of the charging station during the day and maximizing the loading factor of the charging station itself. These two goals will create a trade-off. When the charging station wants to obtain higher charging revenue, the charging station's planning of the charging rate for each time period may cause a decrease in the charging station's daily load factor; conversely, when the charging station's daily load factor is to be increased, the charging station will be charged. The decline in earnings. Therefore, how to find the optimal solution to find the optimal solution in this framework of the trade-off problem by changing the charging rate of the charging station for household electric vehicles in each period is the focus of this research. 3.3 Multi-objective immune algorithm In the multi-objective optimization problem in this paper, the two objective functions conflict with each other, so it is impossible to find a solution that can optimize both targets at the same time. The solution to the multi-objective optimization problem is called the Pareto optimal solution. Its characteristic is that when the performance of any objective function is improved, the performance of another objective function must be reduced [17][18 ]. In solving multi-objective optimization problems, multi-objective immune algorithm [19] has outstanding convergence and diversification advantages in decorrelation problems, making multi-objective immune algorithm gradually become one of the popular multi-objective evolutionary algorithms. Multi-target immune algorithms mimic the human immune system and mimic the mechanisms that produce antibodies. The human immune system produces the corresponding antibodies after detecting the virus. In addition, the immune system also has the ability to remember, when the same attack, automatically generate the corresponding antibody to resist attacks. This feature can be used to speed up the convergence of the algorithm. In the problem of multi-objective optimization, the objective function can be regarded as an antigen (Antigens), and the antibody produced by the immune system can be regarded as a solution to the multi-objective problem. The fitness of the antibody to the antigen corresponds to the suitability of the solution and the objective function. The obtained solution will exist in the same memory cell set, and the evenly distributed Braydo optimal solution can be obtained through continuous updating and iteration. 4 Simulation results and discussion This paper simulates a charging station's charging situation for one day, and Fig. 4 is obtained by simulation, including 30 Braydo optimal solutions. Since the remaining battery power is generated by the random variable when the household electric vehicle enters the charging station, the result of each simulation will be slightly different. Fig. 4 The optimal Beredo optimal solution obtained by multi-objective immune algorithm After obtaining the Beredo set, in order to find a better load factor and charging revenue acceptable to the charging station, we must solve this multiple criteria decision making problem. Multi-criteria decision-making is to help decision-makers analyze and screen different criteria in a limited number of scenarios, and finally select a solution that meets the expectations of decision makers. In the multi-criteria decision-making approach, we use the Manhattan Manhattan Distance (MMD) approach to decision making [20]. The Manhattan Shortest Distance Method is the final output that selects the solution with the shortest Manhattan distance from the ideal vector in the frontier of Beredo. Fig. 5(a) shows that the charging station charges the household electric vehicle with a fixed charging rate of 10 kw/h, and obtains the load amount for each period of the day. The total revenue of the charging station for one day was calculated by the pricing method in Table 1 to be $1,208. Fig. 5(b) shows that the charging station obtains the load amount for each period of the day after optimizing the charging rate using the multi-objective optimization method. The total revenue of the charging station for one day was calculated by the pricing method in Table 1 to be $1,249. Figure 5 Charging station load per day (a) fixed charging rate; (b) optimized charging rate Comparing the load of the charging station before and after optimization is shown in Fig. 6. After finding that the charging rate of the charging station is optimized, the peak power consumption is significantly reduced, and the power consumption during the peak period is increased, and the power consumption is relatively average in each period. The load factor increased from 0.413 to 0.476, an increase of 15.3%. The total revenue of the charging station for one day also increased from $1,208 before optimization to $1,249, and the revenue increased by 3.4%. This result shows that the multi-objective optimization method proposed in this study can effectively control the charging rate of electric vehicles in the smart grid, thereby increasing the load factor and revenue of the charging station. Figure 6 Charging station before and after optimization 5 Conclusion In the smart grid environment, if the charging station as the underlying power system only considers how to increase the revenue when it supplies power to the user, it is possible to make the load factor at a lower state. In order to increase the stability of the power grid, the service revenue and load factor of the charging station are used as the objective function of multi-objective optimization, and then the optimal solution is obtained by the multi-objective immune algorithm. The simulation results show that after using this optimization algorithm, the charging station can simultaneously increase the service revenue and load factor of the charging station for one day. Fully Transparent Liquid Crystal Display Fully Transparent Liquid Crystal Display,Industrial Instrument Lcd Display,Household Appliances Lcd Display,Fire Facility Instrument Display Dongguan Yijia Optoelectronics Co., Ltd. , https://www.everbestlcdlcms.com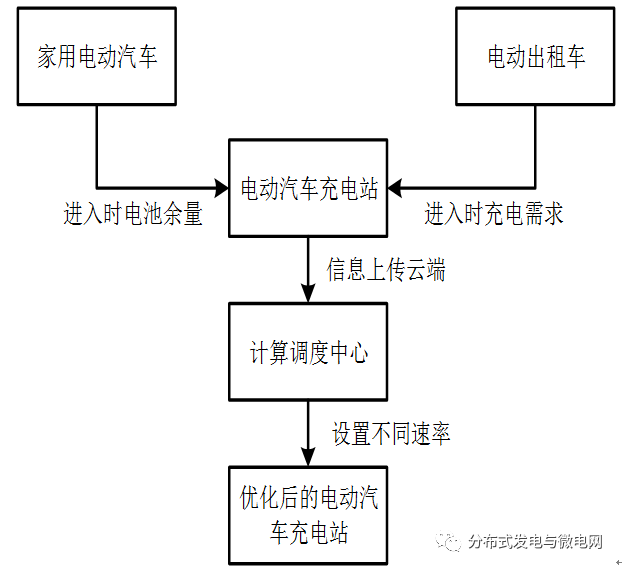

February 15, 2023